第一类：简单题。特点是信息量小，条件单纯。

　　比如30-31题基于以下题干

　　某工厂有一员工宿舍，住了甲、乙、丙、丁，戈、己、庚7人，每人毎周轮流值日一天，且每天仅安排一人值日。他们值日的安棑还需满足以下条件：

　　(1)乙周二或者周六值日;

　　(2)如果甲周一值日，那么丙周三值日且戊周五值日;

　　(3)如果甲周一不值日.那么己周四值日且庚周五值日：

　　(4)如果乙周二值日，那么己周六值日。

　　30.根据以上条件，如果丙周日值班，則可以得出以下哪项?

　　(A)甲周日值班(B)乙周六值班(C)丁周二值班(D)戊周二值班(E)己周五值

　　这类题既有综合推理的特征，又有复言推理的知识，属于简单题。它重点考查演绎推理的知识，而如果有难点的话，一定在信息的排列组合上。答案为B，解法不难，这里就不做解释了。31题略。

　　再如第35题，47-48题，都属于这类型的比较简单的综合推理题。对于这些题来说，只要你在基本的演绎推理上不出问题，知识与技巧熟练的话，那么这5题是很容易拿下的。10分，其实就是这么容易的得到了，只是须要那么一点点静心而已。

　　当然，这类型的题目里也会有些相对比较难一点点儿，比如40-41题的第41题。

　　40-41题基于以下题干

　　某海军部队有甲、乙、丙、丁、戊、己、庚7艘舰艇，拟组成两个编队出航，第一编队编列3艘舰艇，第二编队编列4艘舰艇，编列需满足以下条件：

　　(1)航母己必须编列在第二编队：

　　(2)戊和丙至多有一艘编列在第一编队：

　　(3)甲和丙不在同一编队

　　(4)如果乙编列在第一编队，则丁也必须编列在第一编队。

　　41.如果丁和庚在同一编队，则可以得出以下哪项?

　　A.甲在第一编队B.乙在第一编队

　　C.丙在第一编队D.戊在第二编队

　　E.庚在第二编队

　　从题干所给条件来看，它给的条件也是以演绎为主，理应是一道简单的题目。但由于条件3的存在，使问题会变得相对复杂一点点。

　　

　　由条件1可知：己在第二编队。那么其余的6艘舰艇要平均分配给两个编队，各3艘。

　　第41题增加的条件是：丁和庚在同一编队。那我们就要丁、庚入手。由于没说明它们在第几编队，所以须要假设一下。纵观条件2~4，能够假设的也就只有丁了。

　　由条件4可知，若丁在第2编队，则乙也在第2编队，加上庚，已经3艘了。

　　而由条件3可知：甲、丙中还有一艘在第2编队。

　　这样，第2编队就有4艘舰艇了。但题干说明：第2编队只有3艘，矛盾了。

　　所以，丁和庚只能在第1编队。

　　结合条件3可知，第1编队的第3艘应该是甲、丙中的某艘。

　　所以，乙和戊只能在第2编队。

　　第二类：复杂题。信息量大，以非演绎条件为主。

　　这类题，每年的题量不大，去年为最，而今年只有54-55题，严格来说，只是55题能够算成这类题。也正是这两题，我还是坚持个人的观点，它纯粹不是考查你多时间能把它解出来，而是考查你多长时间可以放弃它，而是把时间花到其它的题目上去。

　　由于今年的这类题放在了最后，因此事实上2018年综管试卷对考生的心理压力并不是太大。而如果前面做的可以的话，在放弃最后一题上还是没多大压力的。

　　比如第54-55题：

　　某校四位女生陈琳、张芳、王玉、杨虹与四位男生范勇、吕伟、赵虎、李龙进行中国象棋比赛。他们被安排在四张桌上，每桌一男一女对弈，四张桌从左到右分别记为1、2、3、4号，每对选物需要进行四局比赛，比赛规定：选手每胜一局得2分，和一局得1分，负一局得0分。前三局结束时，按分差大小排列，四对选手的总积分分别是6：0、5：1、4：2、3：3。已知：

　　(1)张芳跟吕伟对弈，杨虹在4号桌比赛，王玉的比赛桌在李龙比赛桌的右边：

　　(2)1号桌的比赛至少有一局是和局，4号桌双方的总积分不是4:2;

　　(3)赵虎前三局总积分并不领先他的对手，他们也没有下成过和局：

　　(4)李龙已经连输三局，范勇在前三局总积分上领先他的对手。

　　54.根据上述信息，前三局比赛结束时谁的总积分最高?

　　(A)杨虹(B)施琳(C)范勇(D)王玉(E)张芳。

　　55.如果下列有位选手前三局均与对手下成和局。那么他(她)是谁?

　　(A)施琳(B)杨虹(C)张芳(D)范勇(E)王玉。

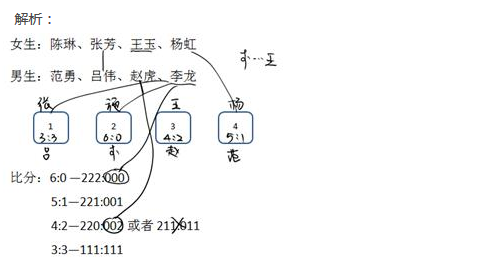
　　解析：

　　首先，此题所给信息有分类的特征，如右侧的男生、女生两行。

　　其次，还有排列序，如左侧4张桌子。

　　最后，还有数字，先做分析，如左侧图示。

　　随着读条件，把能够标示的修订稿，在左侧的图里进行标示。比如：连上“张芳和吕伟”。

　　由条件4可知，李龙就是6:0里的那个0.

　　由条件1可知：李龙在王玉的左边，所以只能在1或2号桌上。

　　由条件2可知，一号桌有和局，而李所在的桌是6:0，没和局，所以李只能在2号桌。

　　由于王玉在李龙的右边，所以王玉只能在3号桌。由于可以推知：张芳、吕伟在1号桌。

　　由条件3可知，赵虎没下过和局，所以他所在的桌的比分不是5:1、3:3，而只能是4:2。

　　由条件2可知，1号桌有和局，其比分不是4:2，而4号桌也不是4:2，那么只能是3号的比分为4:2了。而赵虎也在3号桌。

　　至此，8个人的位置也就推算完了。结果如图所示。第54题的答案就出来了，B为答案。

　　在些基础，我们再推一步，就能推出55题。由条件4可知，范勇所在的4桌不差距，因而只能是5:1，而第一桌的情况就是3:3了。